Reduction operations in numpy
Written: 26 Aug 2020 by Vinayak Nayak 🏷 ["basics"]This post is written in succession to my previous post on special arrays in numpy. You may have a look at the same here.
It explains the special array types in numpy which are quite handy and help substantially in DL or ML or other miscellaneous Data Science Applications.
Topics covered in this post are as follows
- Introduction
- Descriptive stat reduction operations
- argmax & argmin
- reduce & accumulate operations
Introduction
Numpy arrays have become inexpensible in the world of data science. They offer a wide range of functions which are encountered most often when dealing with data. One such family of functions is the family of reduction operations. Eponymously, reduction operations are the ones which reduce the number of elements in an array.

Just by reading through the definition, we can’t gauge the significance of these operations. Let me give a list of the functions we’re going to look at, then the usability of these functions will become very clear.
- descriptive stats — sum, mean, standard deviation, min, max
- argmax
- argmin
- reduce & accumulate
So, let’s get started.
Just like it says, it sums up the elements of an array. When we’re dealing with a one dimensional array, it’s not anything great, it’s just a simple addition of a few numbers thrown at a computer.
But when we go to higher dimensions, we can see the real power of numpy. We can sum along any given axes of an object. Consider a 2-Dimensional array/matrix for example.
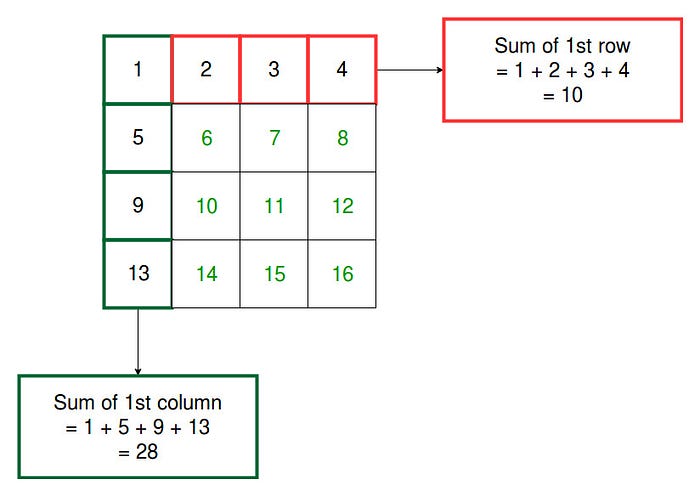
Descriptive Stat Reduction Operations
Mean, standard deviation, minimum, maximum etc. are commonly referred to as descriptive statistics of any given dataset and they’re typically obtained using reduction operations — along row, along column, along third dimension, along nth dimension etc. But effectively they involve compressing the data along a dimension to a single unit by giving up on one of the dimensions — hence reduction. These stats give an idea of the distribution of the dataset and features of the dataset which provide an initial insight into the structure of the data.
Many real world structures/tabular data problems are processed in pandas data-frame which is built on top of numpy arrays. Typically, the rows are records of an individual data-point and the columns are the features of a record. When we want to get an idea of the distribution of features we can use reduction operations like sum over individual axes (particularly the columns). Here’s an example of the same below.
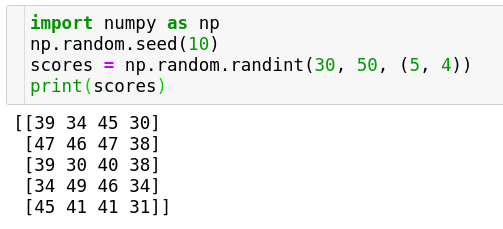
Let’s say the values above are the scores of 5 students in 4 subjects. Here, rows represent students(records) and columns represent marks in a subject(features). We can see the sum of scores of each student by summing over the rows. We can see the sum of scores per subject by summing over the columns. Here’s how we can do the same.

Now let’s say we wanted to focus on the average marks scored by a student, we can reduce the scores array using the mean function in numpy as follows.

We can also focus on the standard deviation of marks scored by students. Standard Deviation is intuitively speaking how bound or spread the distribution of the marks is from the mean score of the students. It measures how dispersed the data is from the mean.

We can see the highest and lowest scores which a student has secured using the min and max functions respectively. They too are as simple to use as the above ones.

Notice the we have always specified the axis argument until now, telling numpy explicitly that we want to reduce along that dimension. Sometimes you’re interested in global reduction, i.e. reduce the entire matrix to a single value. Let’s say you wanted to find the sum of scores of all students in all subjects or, you wanted to find the mean score across all students in all subjects. This can be done by omitting the axis argument altogether. This will then perform reduction across the entire array or matrix.
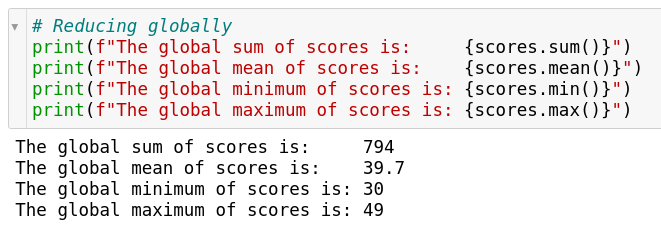
There are two more reduction operations which in addition to the above ones which are of great significance especially in Machine Learning and Deep Learning.
argmax & argmin
Given an array it finds out the index of the maximum or minimum element along a given dimension. Let us consider using the above example itself. Suppose we wanted to find out which student out of the five students scored highest in subject one. We can get the scores for subject one and do an argmax on the same to find this out.
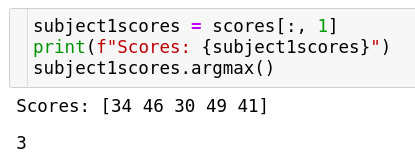
Since indexing starts at 0, we can see from the scores above that 4th student i.e. the 3rd index is where the scores are highest.
Consider that we wanted to find out which student got the lowest marks in subject one. We can do an argmin on the same array to figure that out.
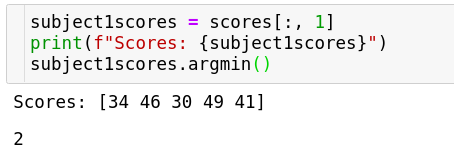
We can find out the same for all the subjects using the entire array and specifying the reduction dimension along the axis. Since we want to reduce across the scores, we’ll specify axis = 0

We can conversely find out which subject did every student performed the best or the worst in by specifying the axis accordingly, we’ll specify axis = 1 for this case and this is how it appears.

In classification tasks in Machine Learning and Deep Learning applications, we always get a probability distribution or likelihood scores of every class for a given input. argmax() function helps to find out the most likely class for that input.
In nearest neighbour search application for eg. picking items similar to a given input item, a distance matrix is calculated and argmin() function helps to find out the nearest neighbours because we’re looking to minimise the distances of the neighbours from the given input item.
reduce & accumulate operations
Numpy provides this function in order to reduce an array with a particular operation. The way these functions work are they repeatedly apply the operation over all the elements of an array until only a single element remains.
The key difference between the two is that reduce function stores only the final result whereas the accumulate function stores all the middle stages of computation as well.
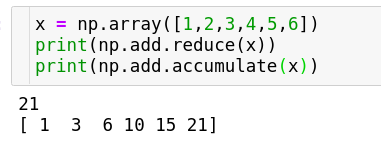
These functions help us in case where we have to perform cumulative operations for eg.
- Finding out the cumulative distribution of a feature.
- Creating elbow charts to determine how many significant components to keep in Principal Component Analysis (a method used for dimensionality reduction in ML)
In this post, we studied about reduction operations in numpy which are very handy in many ML/DL/Data Science operations in general.
The code snippets above can be viewed on my github in this repository Numpy Explained.
In our next post we shall talk about some advanced operations in numpy which are commonplace and will inevitably be used by Data Scientists.
