Basics of numpy

This post aims to give a brief introduction to some important data structures and basic operations in numpy. Topics covered in this post are as follows:

• What is an array object?
• Array Terminologies
• Uses of array objects
• Creating array objects with numpy
• Basic array operations (elementwise operations)

What is an array object?

Simply put, an array is a data structure meant to hold data (generally but not necessarily of similar datatypes) in a particular scheme/format. Formal definition of an array object as per the numpy docs is as follows:

An array object represents a multidimensional, homogeneous array of fixed-size items.

What a recursive definition, or is it? Note that we’re trying to define an array object as defined in numpy and not an array (the definition of an array is already mentioned in the first line of this para: a data-structure holding data in a fixed format). For understanding the definition, we have to first understand all the terms mentioned here. So, let’s start with some intuition from geometry to understand the concept of what dimensions are.

In geometry, fundamental unit/building block is a point which is a zero-dimensional entity. When they’re arranged next to each other, we get a contiguous set of points making a line; this is a one-dimensional entity.

Next, when we arrange a set of lines which are at some angle (other than 0 degrees) to one another, we get a plane which is a two dimensional entity and then sets of planes which define a parallelopiped become a three dimensional entity and so on. Since we’re three-dimensional beings, we can visualize 0, 1, 2 and 3-Dimensional structures but this logic of stacking dimensions can continue perpetually and we call the resulting space n-dimensional space.

The nd-array object in numpy can be thought of a generic object capable of representing data in n-dimensions. You can think of a python list as one dimension. When you nest multiple lists within one another, you create what is an n-dimensional array. (n-dimensional is just another way of saying multi-dimensional).

Now that we have some idea of what a dimension is, let’s tackle the second part. Homogeneous simply means that the lists which we nest to create this structure must all contain same kind of items.

Let’s say you have a box of oranges with oranges aligned neatly with their axes perpendicular to each other. This arrangement is a 3-Dimensional one. However if you got a capsicum sitting in one or more spots in this box, you can’t call this arrangement a 3-Dimensional array. Note that it cannot be called an array because you have dissimilar items in the arrangement. That’s what homogeneous means.

In terms of program, a nested list could be called an array if all elements of all lists are of the same datatype i.e. either int, float, bools, strings or anything. But since we’re doing numerical computation, these types are limited to ints and floats for numpy. And remember that we have to compulsorily wrap it in the np.array function to call it a numpy nd-array object.

Array Terminologies

Rank of an array object

The rank of an array is the number of dimensions present within the array. It’s interesting to note that some arrays have also got special names.

A rank one array is also called a vector, just an array. (Colloquial understanding is that array = 1 dimension).

A rank two array is also called a matrix.

All other arrays are referred to by prepending the rank followed by a D. eg. 3D-array, 4D-array, nD-array etc.

Axis of an array object

The axis of an array is a specific dimension along that array. The elements of an array are said to run along/across axis of an array. The length of an axis is the number of elements running along that axis.

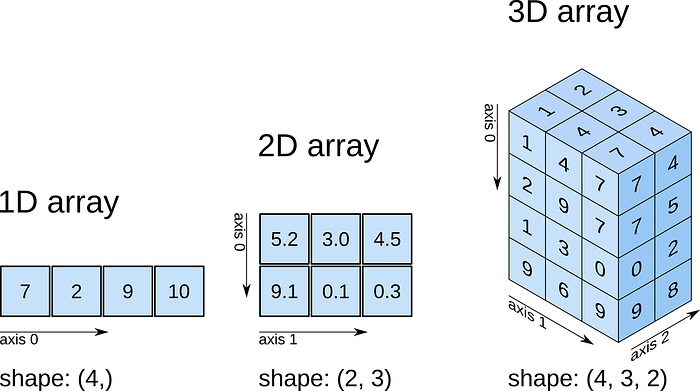
Shape of an array object

The lengths of all the axis together correspond to the shape of an array. If we know the shape of an array, we automatically know the rank and axes as well.

For eg. a 3 X 4 array has rank 2 and the there are two axes which run for a length of 3 and 4 elements respectively.

Uses of Array Objects

Now that we know about what arrays are, let’s first understand how & where they’re useful and then go on to study them in more depth.

To name a few uses of arrays, they’re as follows:

• Any Machine Learning problem involves expressing the output Y as a function of the input X. These inputs and outputs are expressed typically as a 1-Dimensional array or more colloquially referred to as vectors.
• Applications involving checking the states of machines/elements/programs use flags or flag variables which are convenient to be represented as vectors.
• In any natural language processing problem, sentences are represented as sequence of words. A sequence of words is nothing but a 1-D array/vector. Also in time-series analysis, the dependent variable is studied with respect to it’s past values which are also represented as a 1-Dimensional array/vector.
• Images are represented as either 2-Dimensional (monochromatic) or 3-Dimensional (colored) or 4-Dimensional (colored with transparency) arrays of numbers. Any Deep Learning application needs you to specify the image in one of these formats. What you’re viewing on your screen right now as you read this is a 3-Dimensional/4-Dimensional array being rendered as an image in real-time; that’s how important and underappreciated this data-structure called as an array is!

Now that we know why we need arrays, let’s get our hands dirty and understand how we can use them along with numpy.

Creating arrays using numpy

It’s pretty simple to create an array in numpy. You create a list and wrap numpy’s array function around it as follows

import numpy as np
x = [1, 2, 3, 10, 11]
y = np.array(x)

Optionally you can specify the type of data you want your numpy array to be. It could be one of np.int8, np.int16, np.int32, np.int64, np.float16, np.float32, np.float64. The numbers specify the number of bits used to store every element in that array. If you don’t specify, numpy will automatically assign one of np.int64 or np.float64 based on the data you have in the array.

You can see the shape of an array using

print(np.shape(x))

This prints the shape of the array x to the console. Also you can see the rank of an array using

print(len(np.shape(x))

since shape is basically a tuple with the lengths of axes. Apart from this, there are special functions which can create arrays of particular types for eg. An Identity matrix, a diagonal matrix, zeros matrix etc. I will discuss that in a future post.

Basic Array Operations (Elementwise Operations)

Let us discuss some simple fundamental operations which we can do with arrays.

All the basic arithmetic operations like addition, subtraction, multiplication and division can be performed on two arrays having same shape. These operations are carried out in an elementwise manner i.e. corresponding elements in the same position across the two arrays are operated upon.

Unary operations of negation and reciprocal are also done elementwise. Let’s see them in action in code.

Let us start by defining two arrays, each of shape 2 x 2. Data could be any numbers of your choice.

We can simply use the addition symbol for adding two numpy arrays together. Alternatively, you can use np.add(x, y)

We can subtract one array from another using minus symbol or alternatively by using np.subtract(x, y)

Two arrays can be multiplied using the asterisk symbol as shown or by inbuilt function np.multiply(x, y)

Two arrays could be divided elementwise by using either the forward slash or by using np.divide(x, y)

The unary operation of taking a reciprocal can simply be done by performing 1 / arrayname thanks to broadcasting in numpy. I will cover broadcasting in another post, but it simply allows you to do operations without having to particularly bother a ton about the datatypes or shapes of arrays under operation.

Similarly, the unary operation of negation can simply be performed by adding a minus sign in front of the array variable.

The code snippets above can be viewed on my github in this repository Numpy Explained.

In the next post, we will look at some special arrays and functions to create the same.

References

Numpy Documentation